ABSTRACT

A new class of filter, which exhibits broadband matched impedance at its ports, has recently been invented and made available. This new device, the reflectionless filter, has demonstrated a variety of benefits when used to replace conventional filters in a signal chain. This white paper briefly introduces the reflectionless filter and compares conventional filter and reflectionless filter behavior. Use cases are presented examining how reflectionless filters can improve system performance when used with mixers, ADCs, and receiver signal chains. Lastly, an experiment is described and test results presented to compare the conversion loss ripple in multiplier chains when reflectionless and reflective filters are used to filter spurious signals.

INTRODUCTION

The advent of broad bandwidth amplifiers, analog-to-digital converters (ADCs), digital-to-analog converters (DACs), and software-defined radios has brought about growing interest in broadband communications, radar, and sensing applications. For these applications, there is often a need to preserve the highest sensitivity and dynamic range possible within the receiver signal chain and to mitigate the number and strength of harmonics and spurious content in the transmitter signal chain. This is a substantial challenge considering the nature of non-linear components within these circuits, namely compression-mode amplifiers, mixers, multipliers, and frequency-conversion electronics.

A long-overlooked opportunity to enhance the signal-to-noise ratio (SNR) and dynamic range within a signal chain and to reduce harmonics/spurious content within these circuits is to address a seemingly innate property of filters: their out-of-band reflective behavior. Reflectionless filters utilize a novel circuit topology to effectively  eliminate the standing waves created by traditional filters without additional components (such as pads). This unique property gives designers a new way to improve the system performance of a wide array of broadband circuits, or any circuits suffering from out-of-band impedance mismatch.

REFLECTIONLESS FILTER BASICS

A Brief History of the Genesis of Reflectionless Filters

Reflectionless filters were born from a desire to enhance the signal chain performance of sensitive radio astronomy receivers. Innovators of the technology noted that the typical performance of conventional filters (reflective filters) only exhibited a matched impedance at its ports within the filter’s pass-band. The stop-band regions of these filters are intentionally designed to have a very poor impedance match. As a result, undesired stop-band signals, including harmonics, interference, and noise, are all reflected from the filter ports back through the signal chain. If these unwanted signals are reflected back to another reflective device, a standing wave effect emerges. This standing wave will persist and build on itself until the attenuation of the transmission path between the two reflective components dampens and absorbs the unwanted signal energy.

In the case of non-linear devices (amplifiers, mixers, converters, etc.), this standing wave can lead to a number of undesirable effects including:

• Gain compression
• Oscillations
• Proliferation of spurious mixing products
• Unexpected resonances
• Degraded stability
• Degraded dynamic range
• Greater susceptibility to process tolerances/environmental factors
• Biasing issues

Hence, it is often necessary to insert isolators or attenuators (pads) into the signal path to dampen this standing wave effect. However, neither isolators nor pads are an ideal solution for most applications. Isolators are band-limited devices with a large footprint, while attenuators are broadband absorbers that absorb even pass-band signal energy. The increased insertion loss from either of these methods may lead to the need for additional gain in the system, and both solutions add cost, size, complexity, and failure points to the circuit.

A better solution is to design a filter that absorbs signal energy in the stop-band instead of reflecting it. Though absorptive filter technologies have existed for some time, their design and implementation didn’t meet all of the desired criteria for a true conventional filter replacement. Hence, a ground-up design effort culminated in the birth of the reflectionless filter, which is a set of filter topologies and designs that inherently exhibit a broadband matched impedance.

Overview of Reflectionless Filter Theory

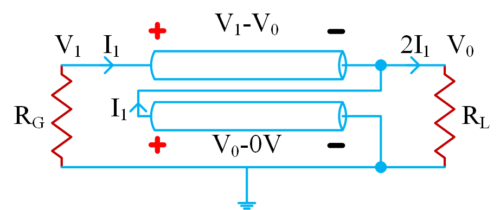
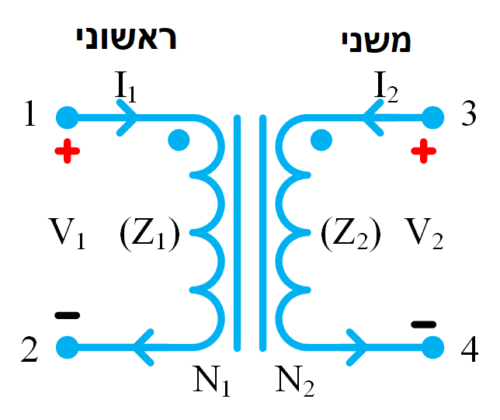
Reflectionless filter topologies are often realized as symmetric networks. This enables the use of even-/odd-mode analysis techniques, which aids in understanding the reflectionless nature of these filters. Given a two-port network with a perfect symmetry plane dividing the circuit, there are two modes useful for analysis. The even mode occurs when both ports are stimulated by signals of equal amplitude and phase, which means there is no current passing across the symmetry plane.

The odd mode occurs when the signals stimulated at either port are equal in amplitude and opposite in phase (180 degrees out of phase), and where the voltage potential at the nodes along the symmetry plane is 0 referenced to ground.

Under these conditions, two separate single-port networks can be drawn, each with only half the elements of the original two-port network with the nodes along the symmetry plane either shorted to ground or open (odd-mode circuits and even-mode circuits). Hence, the scattering parameters of the two-port network can be derived from the superposition of the reflection coefficients of the two circuits detailed in Equations 1 and 2.

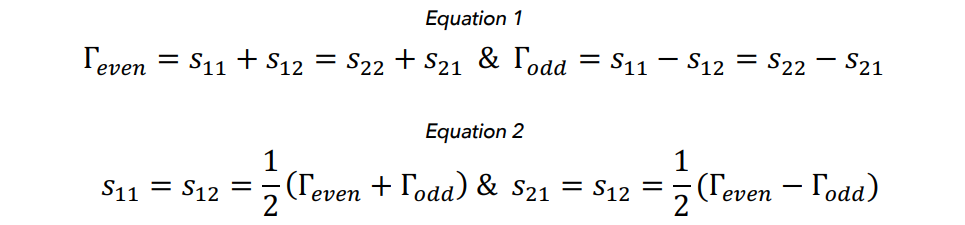
Given the S-parameters, a condition of exact input match (S11 = S22 = 0) can be derived from Equation 3. This condition can only be satisfied if the even-mode and odd-mode circuits are duals of each other (i.e. where their reflection coefficients are additive inverses of one another), which means that the inductors and capacitors, along with the series and shunt elements within each circuit are swapped compared to the other. The result of the combined circuit is a transfer function for the original two-port network equivalent to the reflection coefficient of the even-mode circuit.

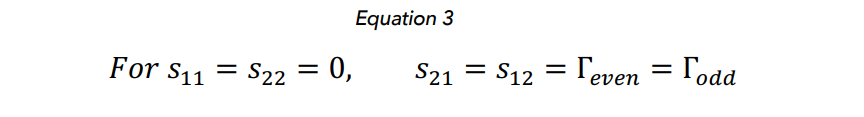
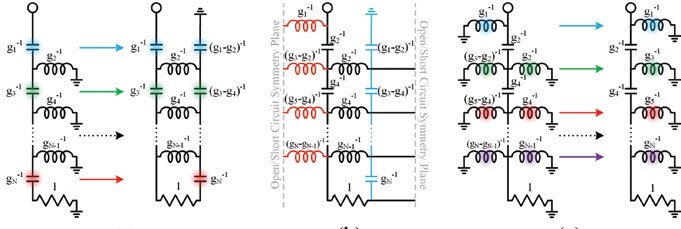
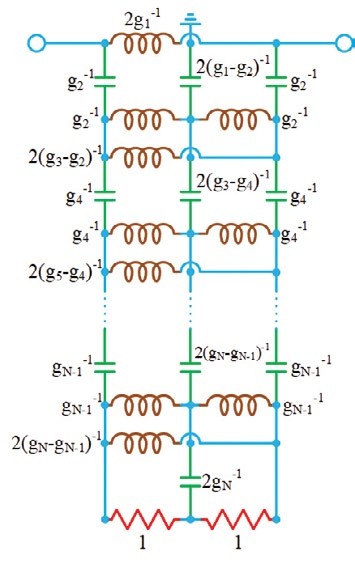
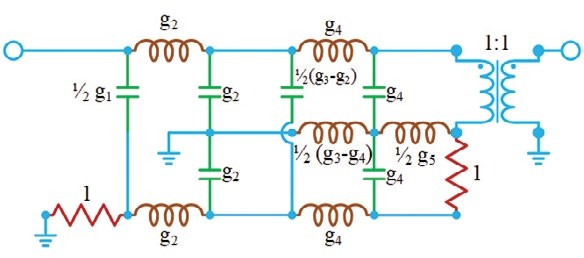
Therefore, low-pass, high-pass, band-pass, and band-stop filters can be generated by choosing a filter topology whose reflection characteristic matches the desired transfer characteristic (even-mode circuit), creating a dual of the chosen filter topology (odd-mode circuit), performing topological modifications that result in symmetry between the even-/odd-mode circuits without affecting the circuit behavior, then combining the two circuit-halves to form the final two-port filter network (See Figure 1 and 2).

It is important to note that for some filter responses, such as Chebyshev, the filter ripple is bounded by the need to maintain positive element values (unless a modification is applied which requires the use of transformers [6]). Hence, for these types of filters there is an additional limit to the stop-band rejection, which means the stop-band rejection only reaches approximately 13-14 dB and is somewhat dependant on the order of the filter. Therefore, when using these filter types to design reflectionless filters it may be necessary to cascade several filters or use a filter response less encumbered by this
restriction (i.e. Zolotarev response).

A Note on Practical Reflectionless Filters

In their current incarnation, reflectionless filters have been mass-produced using a gallium arsenide (GaAs) semiconductor Integrated Passive Device (IPD) fabrication process (see Figure 4). Reflectionless filters with frequency response from hundreds of megahertz to over 30 gigahertz have been realized [9, 10}. A benefit of the GaAs IPD process is that the resulting reflectionless filters are also extremely stable over temperature and exhibit a relatively high operating temperature beyond 100 degrees C.

As with any practical filter, additional loss and parasitics do affect performance relative to the ideal filter circuit. In the case of the GaAs IPD process, the extremely small filters are built with equally compact and planar spiral inductors and capacitors, which have relatively low Q values. Hence, the tradeoff for extremely compact size (3×3 QFN package) and excellent repeatability in these filters is generally greater characteristic insertion loss. However, a benefit of the reflectionless filter topology is that these filters are readily cascadable, so sharper roll-off and greater stop-band rejection may be achieved by adding filters as modular building blocks.

This cascadability allows designers to combine reflectionless filters to achieve the desired response. For example, reflectionless filters may be cascaded to enhance a filter’s stop-band attenuation, extend the stop-band match, or create ultra-wideband (UWB) filters. The examples plotted in Figure 5 show that the stop-band attenuation, which is ultimately limited by the fabrication constraints of the GaAs IPD process, can be improved by combining two complementary low-pass reflectionless filters. Moreover, Figure 6 illustrates that a UWB band-pass filter with a good stop-band match can be achieved by combining a low-pass and a high-pass reflectionless filter.

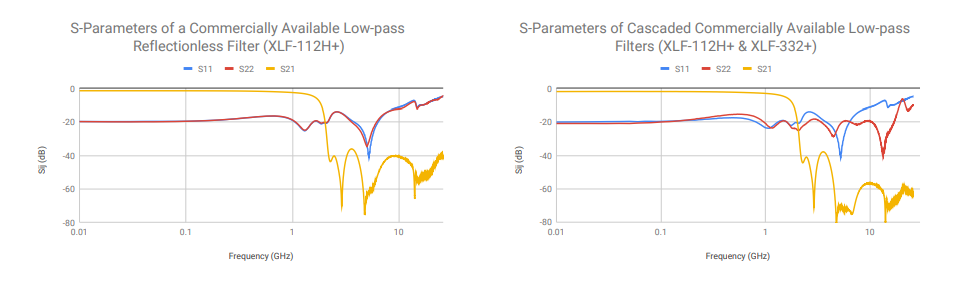
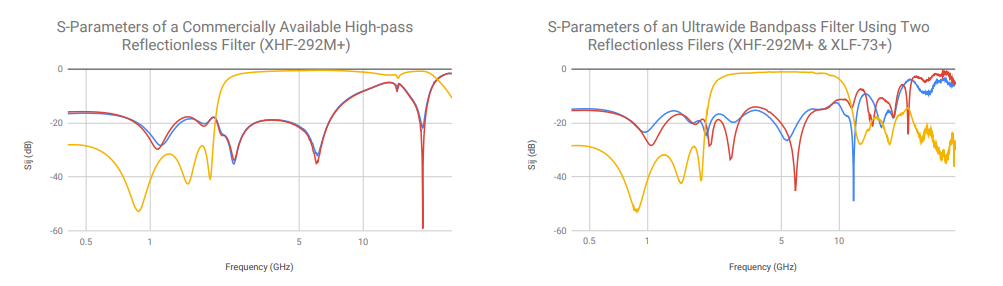
REFLECTIONLESS FILTERS VERSUS CONVENTIONAL FILTERS

It is easy enough to understand the value of having pass-band and stop-band matched impedance at each port of a filter in concept, but it is more instructive to see practical results of the difference between reflective and reflectionless filters in specific implementations. The following examples and discussion revolve around the effects of cascading both reflective and reflectionless filters. Here we examine the negative performance impacts of poor impedance match, compared to filters that are matched at every frequency.

Whereas cascading conventional filters can lead to ripple and cause phase instability in the pass-band, these same concerns are not applicable to reflectionless filters. For example, when comparing conventional filters with reflectionless filters in series, the cascaded conventional filter response will likely suffer from an increased ripple in the stop-band due to an unstable phase relationship between the through and reflected signal. Moreover, a conventional filter will also suffer from additional pass-band ripple as a product of the resulting reflections in the transition. Cascading reflectionless filters, by contrast,  eliminates the distortion and additional ripples common to conventional filters, but creates an expected accumulation of insertion loss (see Figure 7) [10].

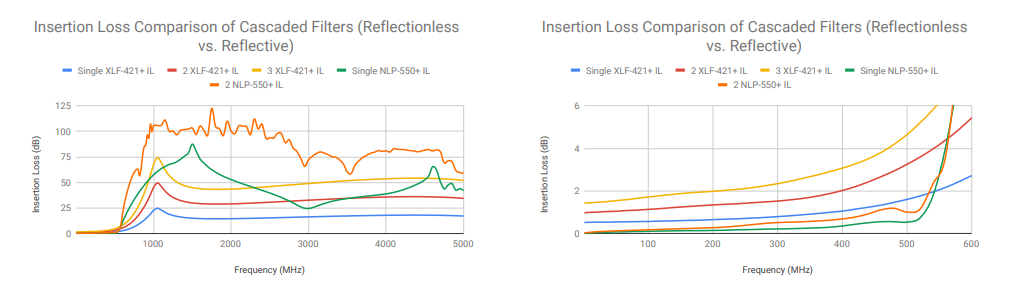
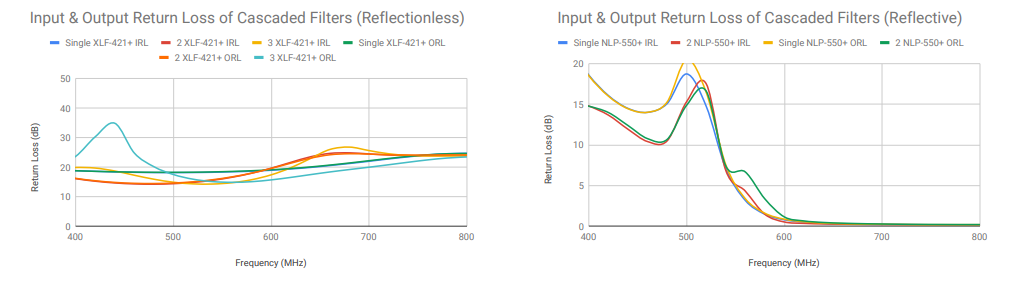
When cascaded, conventional reflective filters also suffer degradation of input and output return loss of the transition corner response due to their poor match in the transition. For example, Figure 8 compares the input and output return loss of cascaded reflective and reflectionless filters. The input and output return loss of just two conventional filter sections in cascade varies significantly around the cutoff frequency. By contrast, the three-section cascaded reflectionless filter exhibits relatively consistent input and output return loss in the pass-band to stop-band transition. This example indicates that where cascading conventional filters degrades the filter’s frequency response (i.e. passband performance), cascading reflectionless filters simply adds a predictable amount of insertion loss without other unwanted effects.

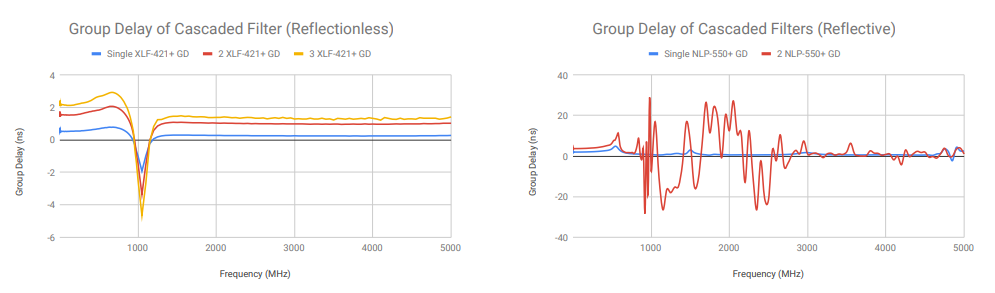
Lastly, the reactive impedance of a conventional filter tends to result in distortion and phase instability, which worsens as filter sections are added. These performance degradations directly impact the group delay performance of conventional cascaded filters (see Figure 9) [10]. Cascaded reflectionless filters, on the other hand, exhibit relatively flat group delay through the pass-band, transition, and stop-band.

REFLECTIONLESS FILTER USE CASES

The following section discusses several applications where replacing conventional filters with reflectionless filters can improve overall system response. Finally, a detailed experiment is presented to illustrate the use of reflectionless filters in multiplier chains and related benefits for system performance.

Pairing with Mixers (Up-/Down-converters) To Improve SNR and Dynamic Range

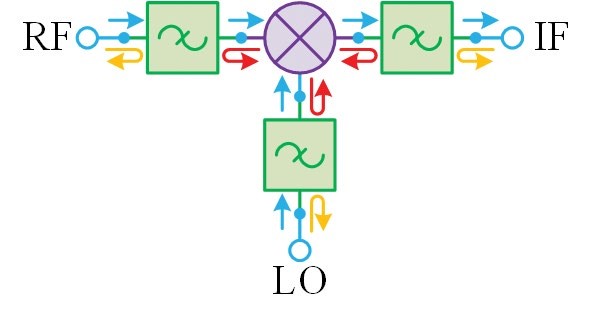
One inherent aspect of a mixer’s non-linear behavior is the creation of undesirable leakage and spurious signals in various areas of the spectrum (images and etc.). Filters are often used to help suppress these unwanted mixer products (see Figure 10). However, at the ports of a mixer, a conventional filter’s stop-band reactive impedance can degrade dynamic range and conversion loss. It can also lead to the development of nulls and increase sensitivity to process variations, phase instability, amplitude instability, expansion of the intermodulation products, and more. Replacing a conventional filter with a reflectionless filter in an anti-aliasing or image rejection application can improve sideband separation, enhance calibration longevity, and mitigate mixer sensitivities to process tolerances. Moreover, a reflectionless filter and mixer pair (if the reflectionless filter is well chosen for the specific mixer) exhibits nearly the same IP3 performance as the mixer alone, which is not the case for conventional filters. Therefore, replacing a conventional filter with a reflectionless filter may allow the use of a mixer with lower intrinsic IP3 while still meeting system specifications, or at least avoid the need for a mixer with higher IP3 to meet the same system specifications.

Wideband ADC Antialiasing Filter

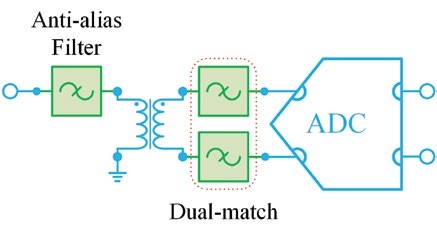
During the sample-and-hold or track-and-hold operations of an ADC, the switching action of the input stage creates a rapid change in the load conditions for the driving circuit. These switching transients may also generate pulses that backpropagate through the system. Though intended for this purpose, the switching transients and other non-linear products may occur at frequencies well beyond the anti-aliasing filter’s operating frequency range. As these filters aren’t intended to be true broadband devices, the impedance matching at these higher frequencies may be poor enough to yield reflections of the switching transients and non-linear products back to the ADC input, create a standing wave and otherwise impact the ADC’s output performance (spur-free dynamic range and noise figure).

In this case, reflectionless filters can be employed at the input of the ADC to absorb the out-of-band signals and mitigate the effect of switching transients. Reflectionless filters can be added to both differential inputs of the ADC, eliminating differential and common-mode switching transients (see Figure 11). If greater selectivity is required than what the typical MMIC reflectionless filters can offer, a traditional anti-aliasing filter with higher Q elements or a cascaded reflectionless filter could be added in series.

Optimizing Receiver Sensitivity and Dynamic Range with a Distributed Filter Approach

Optimizing a receiver signal chain is essential to achieving the desired sensitivity and dynamic range for the system. As is often the case with RF circuits, there is generally a trade-off between sensitivity and dynamic range when attempting to filter out-of-band signals.

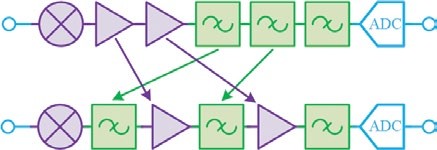
Filtering prior to amplifying the received signal attenuates the out-of-band noise and interference, improving dynamic range. However, this approach also attenuates the strength of the received signal, which reduces the overall receiver sensitivity. Placing the filter after the amplifier allows for greater sensitivity, but reduces dynamic range. It may therefore be desirable to distribute filters with a minimal amount of insertion loss throughout the signal chain.

Unfortunately, cascading conventional (reflective) filters isn’t viable as the out-of-band interactions between the filters can further degrade signal quality. Reflectionless filters, however, can be cascaded without any undesirable side-effects. Hence, a new modular approach of cascading reflectionless filters throughout a signal chain to reach the desired level of sensitivity and dynamic range becomes possible (see Figure 12).

Multipliers and Multiplier Chains: Stabilizing Conversion Efficiency over Frequency

EXPERIMENT

Frequency translation devices such as multipliers and dividers are used to convert frequencies from lower spectrum regimes to higher frequencies, and vice versa. As these devices are intrinsically non-linear, they generate spurious harmonics, which are often filtered to prevent harmonics from appearing in-band. Using conventional, reflective filters creates an undesirable scenario where the out-of-band harmonics are reflected back to the multiplier. The multiplier is also affected by the reactive
loading exhibited by a reflective filter at harmonic frequencies (see Figure 13). Given that multipliers have poor output return loss, this combination of effects leads to large ripples in the conversion efficiency of a multiplier chain, and hence, susceptibility to environmental factors.

As discussed earlier, this issue can be solved by leveraging the unique capabilities of reflectionless filters. In order to demonstrate this solution, an experiment was conducted with a doubler test circuit and a 4X multiplier chain. Each experiment was conducted using comparable reflective and reflectionless filters, and the results were then analyzed (see Figure 14).

The tests were conducted using an Agilent E8257D PSG signal generator and an Agilent U2000A power meter. The doubler used in all tests was a Mini-Circuits ZX90-2-36-S+. The second doubler was a KSX2-24+. The amplifier used in the multiplier chain was a GALI-39+. The conventional filter was a Mini-Circuits VLF-6400+, and the reflectionless filter was a Mini-Circuits XLF-662M+. Each test was done using four different lengths of interconnect between the connectorized doubler and filter: no cable, a 6-inch coaxial cable, a-12 inch coaxial cable, and a 36-inch coaxial cable. An image of the test setup of the doubler-filter pair is presented in Figure 15.

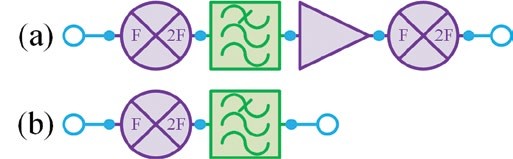
RESULTS

The results of the two experiments are shown in Figures 16, 17, 18, and 19. Figure 16 shows the conversion loss of a doubler filter pair at various power levels with a reflectionless filter (left) and a reflective filter (right). It can be observed from the plots in Figure 16, that even at nominal power levels for the doubler, the reflective filter’s out-of-band impedance mismatch leads to reflections of the harmonics, especially the 3rd harmonic, which leads to greater conversion loss ripple. Figure 17 exaggerates this point by replicating the experiment that produced Figure 16 with a longer transmission line length between the filter and doubler by 6 inches, allowing for greater development of standing waves. Figure 17 shows that the reflectionless filter (left) is able to effectively attenuate the out-of-band reflections with almost no additional conversion loss ripple, while the reflective filter exhibits much worse standing wave effects the longer the transmission line used.

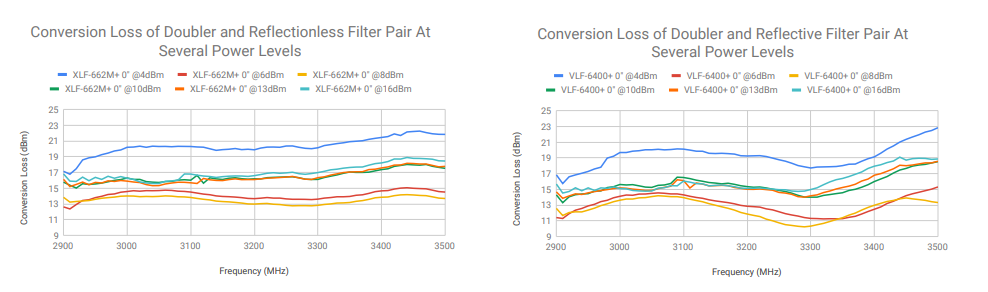
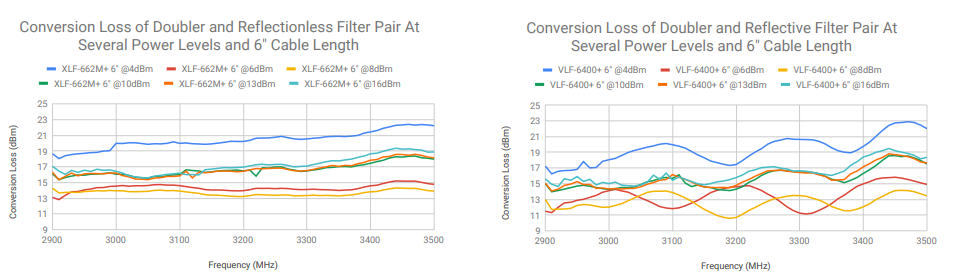
Figure 18 captures the susceptibility of a doubler-filter pair to effects that can worsen the standing waves developed by filters with out-of-band impedance mismatch. Even in the worst-case experimental example (a 36” transmission line extension), the reflectionless filter (left) only develops a marginal conversion loss ripple, while the ripple of the reflective filter (right) is over 2 dB. A side-by-side comparison of the conversion loss ripple for both the reflective and reflectionless filter is provided in Figure 19.

Lastly, in Figure 19 (right) an X4 multiplier chain is tested using two doublers with a filter after the first doubler. This plot shows that the conversion loss ripple under worst-case conditions (extended transmission line) is greater for the reflective filter than the reflectionless filter by over 3 dB peak-to-peak. In order to achieve comparable conversion loss ripple with a conventional filter to that of a reflectionless filter, a much higher power amplifier and an extra attenuator would be necessary to push the doublers well into saturation and mitigate the standing wave generated by the higher power level. In longer multiplier chains, the reflective nature of conventional filters may degrade conversion loss flatness even further and require careful selection of amplifiers and attenuators distributed throughout the multiplier chain, adding size, cost and complexity to the system. By contrast, a well-chosen amplifier with a reflectionless filter can achieve flat conversion loss efficiency while minimizing cost, size and the need for extra components.

CONCLUSION

This white paper has reviewed the basic genesis and theory of reflectionless filters, compared conventional reflective filters and reflectionless filter technology (both theoretically and practically), and described several applications that may benefit from replacing conventional filters with reflectionless filters. An experimental example was also described in detail and test results analyzed to illustrate the benefits of using reflectionless filters with multipliers and in multiplier chains. This discussion has shown several ways that reflectionless filters can overcome many of the typical design challenges associated with introducing reflective filters into a signal chain and in particular the development of standing waves from stop-band signals due to the reactive loading of reflective filters. Reflectionless filters have become a valuable new tool in the RF/microwave engineer’s toolbox, and future developments of reflectionless filter technology may yield even higher performing filtering solutions.